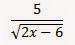Математика по полочкам: 8. Выражения и их преобразования

МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ

Рациональной алгебраической дробью называется выражение вида

, где P и Q - многочлены или одночлены. Множество значений переменной, при которых знаменатель отличен от нуля, называют множеством допустимых значений алгебраической дроби.

Свойства

УПРАЖНЕНИЯ

1. а) Выпишите общий знаменатель дробей:

1) 9x²y; 2) xy; 3) 18x²y; 4)3yx; 5)6x.

б) Выпишите общий знаменатель дробей:

1) xy; 2) x; 3) 8x²y; 4) 4y; 5) 24x²y.

Решение:а) Рассмотрим знаменатели дробей 9x²y, 2х и 3у. НОК(9,2,3)=18; НОК(х, x² )=x² ; НОК(у,у)=у. Тогда общий знаменатель 18x²у.
Ответ: 3).

2. а) Из чисел 4; 1; 0,5; 3; -6; 0 выберите числа, входящие в область определения выражения

б) Из чисел 3; 2; 0,1; -3; 6; 0 выберите числа, входящие в область определения выражения

Решение:
а) Найдем область определения нашего выражения: 3х-6>0, x>2, т.е. D=(2; +∞). Числа, которые входят в область определения: 3, 6.
Ответ: 3,6.

3. Выполните вычитание:

Решение:а) Приведем выражение к общему знаменателю (х+1), для этого домножим вычитаемое на (х+1):

4. Представьте выражение в виде дроби:

Решение:

5. Упростите выражение:

Решение:

Ответ: 2,7х

6. Выполните деление:

а) (42x⁶y³-14x⁴y⁵+7x³y²):(7x²y);

б) (27x¹²y⁴-12x⁸y⁶+9x⁴y⁵):(3x⁴y⁴).

Решение:а)Разделим каждое слагаемое из первой скобки на 7x²y:
(42x⁶y³-14x⁴y⁵+7x³y²):(7x²y)= 6x⁴y²-2x²y⁴+xy.

7. Разложите на множители:

а) 5a²b²-45a²c²; б) 3a²b²-48a²c².

Решение:а)Вынесем общие множители 5 и a²за скобки: 5a²(b²-9c²), воспользуемся формулой разность квадратов: 5a²(b-3c)(b+3c).

Ответ: 5a²(b-3c)(b+3c).

8. Сократите дробь:

Решение:а) Вынесем в числителе общий множитель 3х и в знаменателе - 3:

9. Сократите дробь:

Решение:а) По теореме Виетта корни в числителе 3 и -2 (х1*х2=-6 и х1+х2=1), корни в знаменателе 3 и 2 (х1*х2=6 и х1+х2=5). Зная корни разложим числитель и знаменатель на множители:

10. Выполните действия:

Решение:

11. Сократите дробь (№ 2.4.57 [7]):

Решение:а) Воспользуемся равенством

12. а) Докажите, что при любом значении x значение выражения (5-х)(5+х) - 26 отрицательно.

б) Докажите, что при любом значении x значение выражения (4+х)(х-4) +17 положительно.

Решение:

а) (5-х)(5+х) - 26 =25- x²-26=-x²-1<0, т.к. -x² - отрицательное число и из него вычтем 1, получим отрицательное число.

13. Упростите выражение:

Решение:

а) Разложим на множители квадратные трехчлены:

х²-3х+2=0, D=1, x₁=2, x₂=1. х²-3х+2=(x-1)(x-2).

3х²+7х-10=0, D=169, x₁=-10/3, x₂=1. 3х²+7х-10=3(x-1)(x+10/3)=(x-1)(3x+10).

9х²+4х-5=0, D=196, x₁=5/9, x₂=-1. 9х²+4х-5=9(x+1)(x-5/9)=(x+1)(9x-5).

Ответ: 4-9x, где х≠1, х≠-1, х≠-10/3.

14. Разложите на множители:

Решение:
а)

15. Упростите выражение:

Решение:

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Верно ли равенство:

a) (x-7)(x-2)=x²+9x+14; б) x²-8x+15=(x-3)(x-5)?

2. Запишите в виде алгебраического выражения:
а) произведение полусуммы чисел a и b и числа z;
б) частное от деления числа а на полуразность чисел m и n.

3. Упростите выражение -3х(2х+у) - 4у(3х-2у) и найдите значение полученного выражения при х=-1, у=2.

4. Упростите выражение: