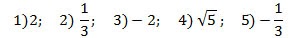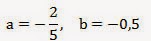6. Одночлены. Многочлены

МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ

Числовое выражение можно составить из чисел, знаков действий и скобок.

Выполняя действия, указанные в выражении получим число - значение выражения.

Если в выражении встречается деление на нуль. то выражение не имеет смысла.

Примеры числовых выражений:

---

Выражение с переменными - это выражение, содержащее переменные. Значение такого выражения зависит от значений переменных.

Примеры выражений с переменными:

При некоторых значениях переменных выражение с переменными может не иметь смысла.

Например:

не имеет смысла при х=-5, т.к. знаменатель не может быть равен 0.

Множество значений переменных, при которых выражение с переменными имеет смысл, называется областью определения этого выражения.

Два выражения называются тождественно равными, если при всех значениях, входящих в них переменных, принадлежащих области определения, соответствующие значения этих выражений равны.

Равенства, верные при всех допустимых значениях переменных, называются тождествами.

Например:

---

Одночлены

Одночленом называется выражение, представляющее собой произведение чисел, переменных и их степеней.

Например:

5x²y⁴;   2,6ab⁵;  -6x^4.

Стандартным видом одночлена называется произведение, составленное из числового множителя (коэффициента) и степеней различных переменных.

Степенью одночлена стандартного вида называется сумма показателей степеней переменных.

Например:

5x²y⁴  - одночлен 6-ой степени, т.к. 2+4=6;   2,6ab² – одночлен  3-ой степени, т.к. 1+2=3.

Одночлены, которые отличаются только числовым коэффициентом или равные между собой, называются подобными.

Например:

5x² и 6х²;   0,25у⁴  и 5у⁴;   3х²у³ и 6х²у³.

---

Многочлены

Многочленом называется сумма одночленов.
Например:

4a³ + 5ab – 2b⁴ + 3a

Если в многочлене все одночлены записаны в стандартном виде и приведены подобные слагаемые, то многочлен называется многочленом стандартного вида.

Степенью многочлена стандартного вида называется наибольшая степень входящего в него одночлена.

Например:

4a³b²c + 5ab – 2a⁵b⁴ + 3a.

Степень одночлена  4a³b²c - (3+2+1)=6;

Степень одночлена 5ab - (1+1)=2;

Степень одночлена 2a⁵b⁴ - (5+4)=9;

Степень одночлена 3a  - первая.

Ответ: многочлен девятой степени.

Чтобы привести подобные слагаемые, достаточно сложить их коэффициенты и полученное число умножить на буквенное выражение.

Например:

5x²y + 4xy² – 6x²y +2xy² = (5-6)x²y + (4+2)xy² = -x²y+6xy².

Чтобы умножить многочлен на одночлен, достаточно каждый член многочлена умножить на одночлен и полученные произведения сложить.

Например:

(x-2y)×2x=2x×x – 2x×2y=2x² – 4xy.

Чтобы умножить многочлен на многочлен, надо каждый член первого многочлена умножить на каждый член второго многочлена и полученные произведения сложить.

Например:

(x – y)(2x+3y-1)=x×2x +x×3y -x×1-y×2x -y×3y +y×1 = 2x² +3xy –x -2xy-3y² +y = 2x² +xy –x -3y² +y.

---

УПРАЖНЕНИЯ

1. а) В результате возведения в квадрат выражения 4х³ получится выражение:

         1) 5х⁶;   2)16х³;   3)16х⁶;    4)4х⁹;    5)16х⁹.

   б) В результате возведения в квадрат выражения 5х⁴ получится выражение:

         1) 5х⁸;   2)25х⁴;   3)25х⁸;    4)5х¹⁶;    5)25х¹⁶.

Решение:
а) (4х³)²=  4²(х³)²=16х⁶.
Ответ: 3)

---

2. а) Известно, что  x⁴<x³, тогда число х может быть равно: 

    б) Известно, что  x⁶>x⁵, тогда число х может быть равно:

Решение:

а)

Ответ: 2)

---

3. Выпишите одночлен, записанный в стандартном виде:

    а) 5aabc;    4x⁵z²a³;   -2x4y³;   6-2x³;   35x⁷y²yz.

     б) d⁴a³ba;    2a⁵b²a³;   -2x⁴y³;   2b³+3;   17c⁷y²cz.

Ответ:

а) 4x⁵z²a³

---

4. a) После раскрытия скобок в выражении -3(3a - 2b) получится выражение:

    1) -9a-6b;   2) -9a+6b;   3) -9a-2b;   4) -9a+2b.

    б) После раскрытия скобок в выражении -5(a - 3b) получится выражение:

    1) -5a-15b;   2) -5a+15b;   3) -5a-3b;   4) -5a+3b.

Решение:

а)-3(3a - 2b)=-3×3a-(-3)×2b=-9a+6b

Ответ: 2)

---

5. Укажите выражение, имеющее смысл при любых значениях переменной х:

Решение:

---

6. а) Укажите выражение, тождественно равное дроби 

     б) Укажите выражение, тождественно равное дроби 

Решение:

---

7. а) Приведите к знаменателю 2х-4 дробь:

    б) Приведите к знаменателю 5-2у дробь:

Решение:

а)

---

8. Приведите одночлен к стандартному виду:

a) 5x²y⁴axa⁶be²;   б)  -5a⁷b³bbc²a²b.

Решение:

a) 5x²y⁴axa⁶be²  =5(х²х)у⁴(аа⁶)be²=5x³y⁴a⁷be². 
 Ответ: 5x³y⁴a⁷be².

---

9. Найдите разность многочленов:

а) 5x²y + xy² -3  и 4xy² – x²y +1;    б)  3a⁶b² – ab² +3   и 4ab² – 7a⁶b² -2.

Решение:

а) 5x²y + xy² -3 – ( 4xy² – x²y +1)= 5x²y + xy² -3 – 4xy² + x²y -1= ( 5x²y+ x²y)+( xy²–  4xy²)+(-3-1)= 6x²y- 3xy²-4.

Ответ: 6x²y- 3xy²-4.

---

10. Представьте в виде одночлена стандартного вида:

a) (-5x²y³)³×4x²y;   б) (2a²b⁵)²×6a⁶b³.

Решение:

a) (-5x²y³)³×4x²y=(-5)³(x²)³(y³)³×4x²y=-125x⁶y⁹4x²y=(-125×4)(x⁶x²)(y⁹y)=-500x⁸y¹⁰.

Ответ: -500x⁸y¹⁰.

---

11. Найдите область определения выражения:

Решение:
а) Выражение под корнем должно быть неотрицательным, т.е. 3х-1≥0, значит х≥1/3.
Ответ: D=[1/3; +∞)

---

12. Упростите выражение:

Решение:
а) Представим все дроби в виде обыкновенных дробей и раскроем скобки:

Ответ: -a-0,2b.

---

13. Упростите выражение и найдите его значение при 

а)

б)

Решение:
а) Раскроем скобки и приведем подобные слагаемые:

Ответ: -10

---

14. Представьте в виде многочлена стандартного вида:

а) 5x + (6-(y-(3y+5)));

б) 4x-(3y+(7y-(3-x))).

Решение:

а) Раскроем скобки и приведем подобные слагаемые: 5х+6-у+3у+5=5х+2у+11.

Ответ: 5х+2у+11.

---

15. а) Упростите выражение и найдите его значение при х=0,5 и у=-0,2:

      (3x+2y)(4x-y²) – (x+y²)(10x-3y);

      б) Упростите выражение и найдите его значение при х=-0,5 и у=0,2:

      (4x-2y)(3x+y²) – (6x-y²)(2x+2y).

Решение:

а) умножим многочлен на многочлен и приведем подобные слагаемые:

(3x+2y)(4x-y²) – (x+y²)(10x-3y)= 12х²-3ху²+8ху-2у³-10х²+3ху-10ху²+3у³= 2х²-13 ху²+11ху+ у³,

Подставим х=0,5 и у=-0,2:    2(0,5)²-13 (0,5)(-0,2)²+11(0,5)(-0,2)+ (-0,2)³=0,5-0,26-1,1-0,008=-0,868.

Ответ: -0,868.

---

16. а) Докажите, что при любом натуральном значении переменной значение выражения   (а+5)(а-6) - (а-2)(а+15) кратно 14.

      б) Докажите, что при любом натуральном значении переменной значение выражения  (а-1)(а+12) - (а-3)(а+4) кратно 10.

Решение:

а) Раскроем скобки и приведем подобные слагаемые:
(а+5)(а-6) - (а-2)(а+15)=a²-6a+5a-30-a²-15a+2a+30=-14a; выражение делится на 14, т.к. один из множителей делится на 14.

---

17. Докажите тождество ( № 2.5.4 [7]):

      a)  (x⁴ + y⁴ –z⁴ + 9xyz)(x⁴+y⁴-z⁴-7xyz) – (x⁴+y⁴-z⁴)(x⁴+y⁴-z⁴+2xyz) = -63x²y²z²;

      б)  (x³ - y³ +z³ - 4xyz)(x³-y³+z³+3xyz) – (x³-y³+z³)(x³-y³+z³-xyz) = -12x²y²z².

Решение:
а) раскроем скобки и приведем подобные слагаемые в левой части равенства:

Что и требовалось доказать

---

18. а) Известно, что x²+y²=3. Найдите значение выражения 5(x+1)(y+1) - (y+x)(x+y+5) - 3xy;
     б) Известно, что a²+b²=-3. Найдите значение выражения 4(b-1)(a+1) + (b-a)(b-a-4) - 2ab.
Решение:
а) раскроем скобки и приведем подобные слагаемые: 5(x+1)(y+1) - (y+x)(x+y+5)-3xy= 5xy+5x+5y+5-xy-y²-2y-x²-xy-5x-3xy= -y²-x²+5=-(y²+x²)+5=-3+5=2.

Ответ: 2.

---

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1.Выберите выражения. не являющиеся одночленами: 2a+bc;  13a; 2a-b; 2x:y; 2x²y².

2. Укажите, какие из равенств являются тождествами:

10+(x+c)=10+x+c;  (6a+12):6=a+2;   a+x=ax; -2(a+b)=-2a+2b.

3. Упростите выражение:

а) 3(x-2y)-0,5(2x+3y)-4,5;    б) 4(a-3b)-1,5(4a+5b)+6,5b.

4. Приведите подобные члены:

a) a²b – 4a² - 5a²b + 4a²+7a²b;    б) 4xy² – y² – 3xy² + 7y² + 9xy².

5. Докажите тождество:

6. Упростите выражение:

7. Найдите значение выражения, зная, что 

8. Верно ли равенство:

a) (x+3)(y+3)=(x+3)(x-y)+(y+3)² при х=5,5, у=5,5;   

б) (x+1)(y+1) = (y+1)²+(x-y)(y+1) при х=-0,7, у=0,7?

9. Докажите, что при любых значениях х и у значение выражения является положительным числом:(x+y)² +2(x+y+1).

10. Упростите выражение:

---

ПРОВЕРЬТЕ СЕБЯ

---